As Redes Neuras São Exemplos De Algoritmos Do Paradigma Estatístico – As Redes Neurais São Exemplos De Algoritmos Do Paradigma Estatístico. Este fato fundamental permeia todo o funcionamento dessas poderosas ferramentas de inteligência artificial. A aparente complexidade das redes neurais, com suas múltiplas camadas e conexões, esconde uma base matemática elegante e profundamente enraizada em princípios estatísticos. Aprenderemos como a probabilidade, a inferência e métodos estatísticos clássicos como regressão são essenciais para o treinamento e a performance dessas redes, permitindo que elas aprendam padrões complexos a partir de dados brutos.
Desde o perceptron simples até as arquiteturas avançadas de redes convolucionais (CNNs) e recorrentes (RNNs), o processo de aprendizado se resume à busca por parâmetros que minimizem uma função de custo, expressa frequentemente como uma medida de erro estatístico. A propagação retroativa, um algoritmo crucial nesse processo, ajusta iterativamente os pesos da rede com base na análise de erros, refletindo a natureza iterativa e probabilística da inferência estatística.
Exploraremos diferentes arquiteturas e seus algoritmos correspondentes, ilustrando a forte ligação entre a estatística e a inteligência artificial moderna.
Redes Neurais e o Paradigma Estatístico: Uma Conexão Essencial: As Redes Neuras São Exemplos De Algoritmos Do Paradigma Estatístico
Redes neurais artificiais, inspiradas no funcionamento do cérebro humano, são ferramentas poderosas de aprendizado de máquina. Sua capacidade de aprender padrões complexos a partir de dados se baseia fortemente em princípios estatísticos. Este artigo explora essa relação intrínseca, desvendando como métodos estatísticos são fundamentais para o funcionamento e o sucesso das redes neurais.
Introdução às Redes Neurais e o Paradigma Estatístico
A relação fundamental entre redes neurais e o paradigma estatístico reside na própria natureza do aprendizado de máquina. Redes neurais aprendem a partir de dados, identificando padrões e relações estatísticas subjacentes. Elas utilizam métodos estatísticos para modelar esses padrões, fazendo previsões e tomando decisões com base na probabilidade. Conceitos como probabilidade, inferência estatística e distribuição de probabilidade são centrais para o treinamento e a avaliação do desempenho de uma rede neural.
Por exemplo, em uma rede neural usada para classificação de imagens, a probabilidade de uma imagem pertencer a uma determinada classe é calculada com base nos pesos sinápticos da rede, que são ajustados durante o processo de treinamento usando algoritmos baseados em princípios estatísticos. A inferência estatística permite que a rede generalize a partir dos dados de treinamento para dados não vistos, fazendo previsões com base nas probabilidades aprendidas.
Tipos de Redes Neurais e seus Algoritmos Estatísticos
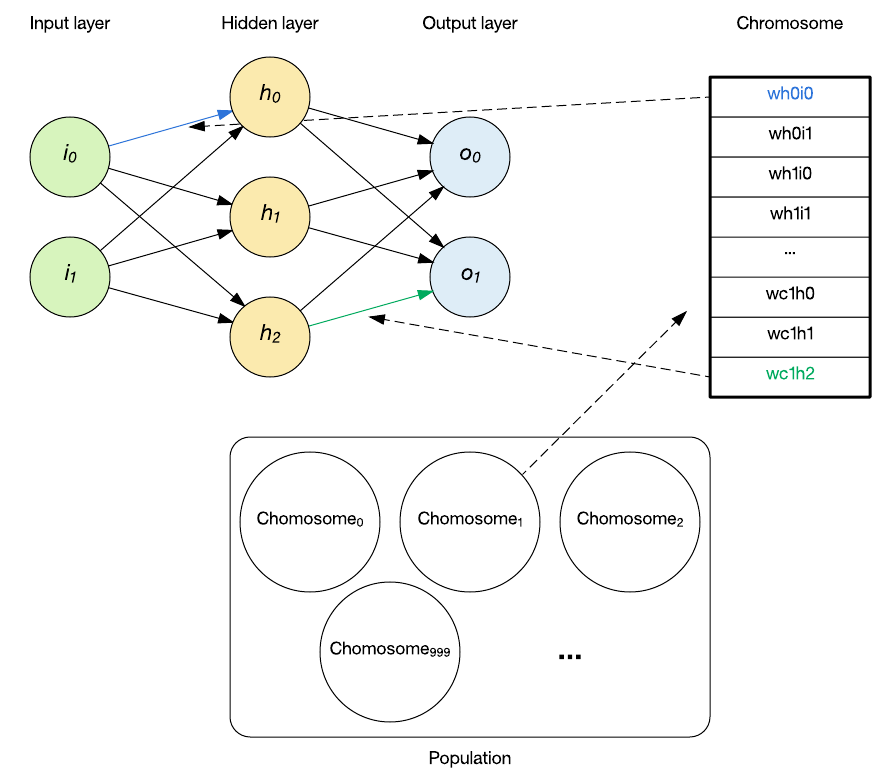
Existem diversos tipos de redes neurais, cada uma com arquiteturas e algoritmos de aprendizado específicos. A escolha do tipo de rede e do algoritmo depende da natureza do problema e dos dados disponíveis. A seguir, comparamos algumas arquiteturas populares e seus algoritmos estatísticos correspondentes.
| Algoritmo | Tipo de Rede Neural | Função de Custo | Método de Otimização |
|---|---|---|---|
| Regressão Logística | Perceptron | Entropia Cruzada | Descida do Gradiente |
| Backpropagation | MLP (Multilayer Perceptron) | Erro Quadrático Médio (MSE) ou Entropia Cruzada | Descida do Gradiente Estocástico (SGD), Adam, RMSprop |
| Convolução | CNN (Convolutional Neural Network) | MSE ou Entropia Cruzada | SGD, Adam, RMSprop |
| LSTM (Long Short-Term Memory) | RNN (Recurrent Neural Network) | MSE ou Entropia Cruzada | SGD, Adam, RMSprop |
Aprendizado de Máquina em Redes Neurais: O Processo Estatístico

O treinamento de uma rede neural é um processo iterativo que envolve a minimização de uma função de custo. Esta função quantifica a diferença entre as previsões da rede e os valores reais. A propagação retroativa (backpropagation) é um algoritmo que calcula o gradiente da função de custo em relação aos pesos da rede, permitindo que esses pesos sejam ajustados iterativamente para minimizar o erro.
Este processo é essencialmente um problema de otimização estatística, buscando os pesos que melhor se ajustam aos dados de treinamento.
A função de custo, frequentemente o erro quadrático médio (MSE) ou a entropia cruzada, mede o quão bem a rede está se saindo na tarefa de previsão. A minimização dessa função é feita através de algoritmos de otimização, como a descida do gradiente, que ajustam iterativamente os pesos da rede para reduzir o erro. O processo é estatístico porque a minimização da função de custo é guiada por estimativas de gradiente calculadas a partir de amostras de dados.
Aplicações Práticas e Exemplos de Redes Neurais Baseadas em Algoritmos Estatísticos, As Redes Neuras São Exemplos De Algoritmos Do Paradigma Estatístico
Redes neurais com algoritmos estatísticos têm inúmeras aplicações em diversos campos. Aqui apresentamos alguns exemplos.
Reconhecimento de imagens: Redes convolucionais (CNNs) são amplamente usadas para reconhecer objetos em imagens. Algoritmos como a convolução e o pooling extraem características relevantes das imagens, enquanto a classificação é feita usando regressão logística ou softmax. Resultados impressionantes foram alcançados em tarefas como classificação de imagens do ImageNet.
Processamento de linguagem natural (PNL): Redes neurais recorrentes (RNNs), especialmente LSTMs e GRUs, são eficazes para processar sequências de dados, como texto. Elas são usadas em tarefas como tradução automática, análise de sentimento e geração de texto. Algoritmos como o backpropagation através do tempo são usados para treinar essas redes.
Previsão de séries temporais: Redes neurais recorrentes e redes neurais feedforward podem ser usadas para prever valores futuros em séries temporais, como previsão de ações ou previsão do tempo. Algoritmos de regressão são comumente usados para modelar a relação entre os dados passados e futuros.
Exemplo de conjunto de dados para treinamento de uma CNN para classificação de imagens: Um conjunto de imagens de dígitos manuscritos (como o MNIST) com características estatísticas como média e desvio padrão da intensidade dos pixels para cada dígito. Para uma RNN em PNL, um conjunto de textos com informações estatísticas como frequência de palavras e n-gramas.
Limitações e Desafios das Redes Neurais baseadas em Algoritmos Estatísticos

Apesar de seu sucesso, redes neurais baseadas em algoritmos estatísticos enfrentam desafios. O problema da dimensionalidade, por exemplo, ocorre quando o número de variáveis é muito grande em relação ao número de observações, dificultando a generalização do modelo. Overfitting, onde o modelo se ajusta muito bem aos dados de treinamento, mas mal aos dados de teste, e underfitting, onde o modelo é muito simples para capturar a complexidade dos dados, são outros problemas comuns.
Técnicas como regularização (L1, L2), validação cruzada e seleção de hiperparâmetros são usadas para mitigar esses problemas. A escolha cuidadosa da arquitetura da rede, dos algoritmos de otimização e dos hiperparâmetros é crucial para obter um bom desempenho. Situações com dados ruidosos, altamente não lineares ou com poucas amostras podem apresentar dificuldades para redes neurais baseadas em algoritmos estatísticos.

